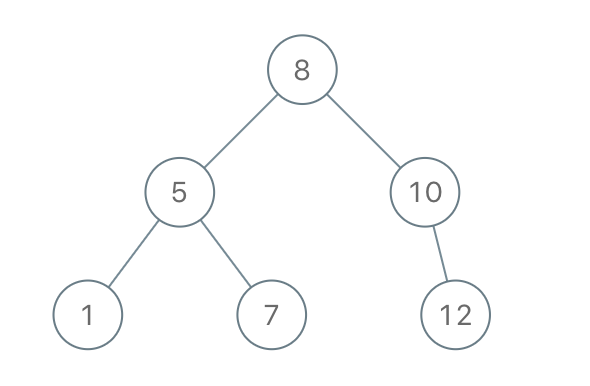
1008.Construct Binary Search Tree from Preorder Traversal
难度:Medium
返回与给定先序遍历 preorder 相匹配的二叉搜索树（binary search tree）的根结点。
(回想一下，二叉搜索树是二叉树的一种，其每个节点都满足以下规则，对于 node.left 的任何后代，值总 < node.val，而 node.right 的任何后代，值总 > node.val。此外，先序遍历首先显示节点的值，然后遍历 node.left，接着遍历 node.right。）
示例：
输入：[8,5,1,7,10,12] 输出：[8,5,10,1,7,null,12]
提示：
1 <= preorder.length <= 100 先序 preorder 中的值是不同的。
先序遍历，先遍历根节点和左孩子，然后到底之后再遍历右边的。不断回溯。
所以当下一个节点比当前节点小时，直接添加左孩子即可。 当其比较大时，不断回溯比较，找到大于该节点的根节点，然后从其左子树开始比较，如果不存在右孩子，则将其添加为右孩子。如果有，则比较其右孩子的右孩子(左边之前已经遍历过了)，不断循环，最后将其添加为右孩子即可。
代码实现如下：
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
TreeNode* bstFromPreorder(vector<int>& preorder) {
TreeNode* root = new TreeNode(preorder[0]);
stack<TreeNode*> s;
s.push(root);
for(int i=1;i<preorder.size();i++)
{
TreeNode* cur = s.top();
if(preorder[i] <cur->val )
{
cur->left = new TreeNode(preorder[i]);
s.push(cur->left);
}
else
{
while( s.size()>1 && cur->val < preorder[i])
{
s.pop();
cur = s.top();
}
if( cur->val < preorder[i]){
while(cur->right)
{
s.push(cur->right);
cur=cur->right;
}
cur->right = new TreeNode(preorder[i]);
}
else{
s.push(cur->left);
cur=cur->left;
while(cur->right )
{
s.push(cur->right);
cur=cur->right;
}
// cout<<cur->val<<endl;
cur->right = new TreeNode(preorder[i]);
}
s.push(cur->right);
}
}
return root;
}
};
执行用时 :4 ms, 在所有 C++ 提交中击败了96.01%的用户
内存消耗 :9 MB, 在所有 C++ 提交中击败了87.58%的用户
