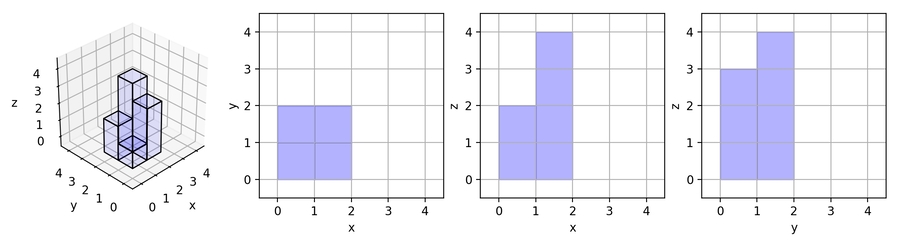
883.Projection Area of 3D Shapes

883.Projection Area of 3D Shapes

难度:Easy

在 N * N 的网格中，我们放置了一些与 x，y，z 三轴对齐的 1 * 1 * 1 立方体。 每个值 v = grid[i][j] 表示 v 个正方体叠放在单元格 (i, j) 上。 现在，我们查看这些立方体在 xy、yz 和 zx 平面上的投影。 投影就像影子，将三维形体映射到一个二维平面上。 在这里，从顶部、前面和侧面看立方体时，我们会看到“影子”。 返回所有三个投影的总面积。

示例 1：

输入：[[2]]
输出：5
示例 2：

输入：[[1,2],[3,4]]
输出：17

解释： 这里有该形体在三个轴对齐平面上的三个投影(“阴影部分”)。

示例 3：

输入：[[1,0],[0,2]]
输出：8
示例 4：

输入：[[1,1,1],[1,0,1],[1,1,1]]
输出：14
示例 5：

输入：[[2,2,2],[2,1,2],[2,2,2]]
输出：21
 

提示：

1 <= grid.length = grid[0].length <= 50
0 <= grid[i][j] <= 50

三视图面积问题，底面面积为矩阵尺度，两个侧面面积分别是行列对比的最大值作为新的一行和一列，加起来就是面积。

class Solution {
public:
    int projectionArea(vector<vector<int>>& grid) {
        int r=grid.size();
        if(!r) return 0;
        int c=grid[0].size();
        int sum=0;
        for(auto x:grid)
            sum+= *max_element(x.begin(),x.end());
        for(int i=0;i<c;i++)
        {
            int mc=0;
            for(int j=0;j<r;j++)
            {
                mc=max(mc,grid[j][i]);
                if(grid[j][i]) sum++;
            }
            sum +=mc;
        }
        return sum;
        
        
    }
};