894.All Possible Full Binary Trees
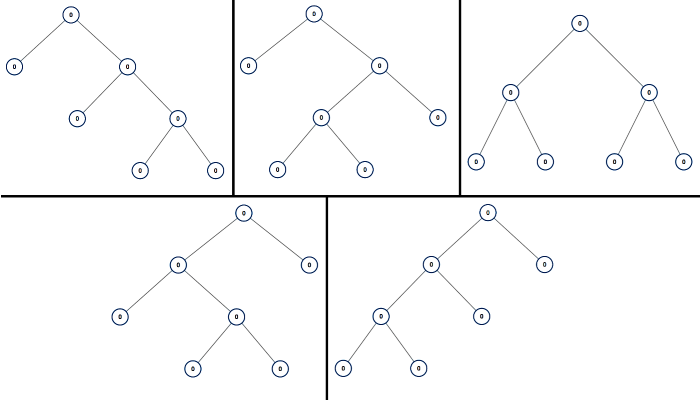
Last updated

Last updated
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
vector<vector<TreeNode*>>allPath;
public:
vector<TreeNode*> allPossibleFBT(int N) {
vector<TreeNode*> res;
if(N%2==0) return res;
TreeNode* zero = new TreeNode(0);
res.push_back(zero);
allPath.push_back(res);
if(N/2+1 <= allPath.size()) return allPath[N/2];
int len=allPath.size();
for(int i=len;i<N/2+1;i++)
{
vector<TreeNode*>tmp;
// cout<<count<<endl;
for(int j=0;j<i;j++)
{
for(auto l : allPath[j])
for(auto r: allPath[i-1-j])
{
TreeNode* root = new TreeNode(0);
root->left = l;
root->right = r;
tmp.push_back(root);
}
}
allPath.push_back(tmp);
}
//cout<<res.size()<<endl;
return allPath[N/2];
}
};